本文译自 Xavier Gourdon 和 Pascal Sebah 的网站,原文http://numbers.computation.free.fr/Constants/Log2/log2.html
log 2 = 0.69314718055994530941723212145817656807550013436025…
通过减少劳动量,使天文学家的寿命翻了一番
– 皮埃尔·西蒙·德拉普拉斯 (1749-1827),关于对数
你不知道,对数表计算有多少诗意!
-卡尔·弗里德里希·高斯(1777-1855),给他的学生.
1 引言
对数的故事开始于苏格兰人约翰·内皮尔(1550-1617)在1614年出版的一本着作中. 这篇论文是拉丁文的,题目是“ Mirifici logarithmorum canonis descriptio” [7]. 不过需要指出的是,瑞士钟表匠约斯特·比尔吉(JostBürgi,1552-1632)独立发明了对数, 但直到1620年,他的作品一直没有发表。.
由于可以分别用加法和减法来代替令人痛苦的乘法和除法,这个发明在欧洲大陆得到了非同寻常的欢迎并迅速传播(特别是得益于像开普勒这样的天文学家的热情)。在内皮尔三百周年纪念展上,乔治·吉布森写道:“对数的发明标志着科学史上的一个时代。
很快,对数表就被发布了. 其中之一是由英国数学家亨利·布里格斯(Henry Briggs)(1561-1631)于1624年出版了他的作品“ 算术对数 ”(Arithmetica logarithmica) [4]。这份对数表精确到十四位数字,并且包含了1-20,000以及9万到101,000的常用对数。. 1628年, 荷兰人Adrian Vlacq(1600-1667)完成了剩余的空缺部分[12]。
数学家更喜欢使用一个所谓自然对数或双曲对数(表示为log或ln,即以e = 2.7182818284 为底的 对数,下面的定义允许简单推导出 对数的主要性质。
定义1 令x> 0
\(log ~x = \int_1^x \frac{dt}{t}=\int_1^{x-1} \frac{dt}{1+t}\)
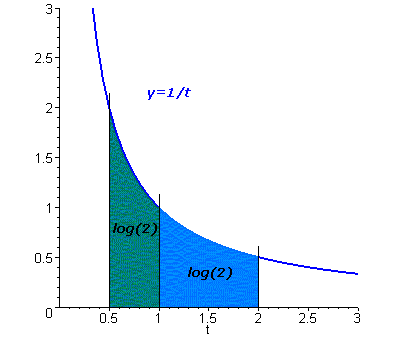
它可被解释为双曲线y = 1 / t下的面积 ,t从1到x. 这个几何解释由耶稣会圣文森(1584-1667))在1647年所展示。
因此,log 2将被定义
\(log~ 2 = \int_1^2 \frac{dt}{t}=\int_0^{1} \frac{dt}{1+t}= \int_0^{1/2} \frac{dt}{1-t}\)
定理2 log 2 是无理数和超越数。
2 基于积分表示的算法
从log 2的积分表示,我们可以推导出一些公式。第一个是从积分的矩形近似(这里h =(b – a)/ n) 推导出来的
\(\displaystyle \int_a^b f(t)dt =h \sum_{k=1}^n f(a+kh) + O(h)\)
对区间[0,1] 应用f(t)= 1 /(1 + t)给出
\(\displaystyle log~ 2 = _{n \to \infty}^{lim} ( \frac{1}{n+1} + \frac{1}{n+2}+ \cdots + \frac{1}{2n})\)
随着这个序列的不断增加。得到的值也越来越精确。
|
x10
|
= | 0.6(687…), |
|
x100
|
= | 0.69(065…), |
|
x1,000
|
= | 0.69(289…). |
这是一个非常缓慢的收敛,但如果我们使用梯形法,则可以改进为
\(\displaystyle \int_a^b f(t)dt=~\frac{h}{2}(f(a)+f(b)+2~\sum_{k=1}^{n-1}f(a+kh))+O(h^2),\)
可得到
\(\displaystyle log~2 = _{n \to \infty }^{lim} \Big ( \frac{3}{4n} + ( \frac{1}{n+1} + \frac{1}{n+2} + \cdots + \frac{1}{2n-1}) \Big ) \)
某些迭代得到
|
x10
|
= | 0.693(771…), |
|
x100
|
= | 0.6931(534…), |
|
x1,000
|
= | 0.693147(243…).. |
其收敛速度有所改善,但仍为对数级收敛。我们现在对积分的计算作出最后的改进,即辛普森法
\( \displaystyle \int_a^b f(t)dt=\frac{h}{6} \sum_{k=0}^n \Big( f(a+kh)+f(a+(k-1)h) + 4f(a+(k-\frac{1}{2})h) \Big)+O(h^4),\)
给出
\( \displaystyle log ~2 = _{n \to \infty} ^{lim} \sum_{k=0}^n ~ \Big( \frac{1}{n+k} + \frac{1}{n+k-1} + \frac{4}{n+k-1/2} \Big) \)
新的迭代得到
|
x10
|
= | 0.693147(374…), |
|
x100
|
= | 0.6931471805(794…), |
|
x1,000
|
= | 0.69314718055994(726…). |
从这些例子中我们可以注意到,这样的公式只能用来计算log 2的少数几位数,因为收敛速度太慢,以致无法得到高精度的常数。
3. 一个简单的极限
有趣的是,我们能够发现,对数可以通过一些非常简单的公式计算出来,这些公式与几何面积没有直接关系,只涉及开平方。
我们知道常数e可以由着名的极限定义来得到
\(e ~= _{n \to \infty}^{lim} ( 1+ \frac{1}{n}) ^ n,\)
值得注意的是,存在一个计算对数常数的类似的公式:
\(log ~ 2 ~ = ~ _{n \to \infty}^{lim} n( 2^{1/n}-1) ,\)
这显然是从那个扩展中推演出来的
\(2 ^{1/n} ~ = ~ e^{ log ~2/n}=1+\frac{log~2}{n} + O(\frac{1}{n^2}).\)
取n = 1000,我们发现
x1,000 = 0.693(387…).
一个更好的公式给出
\(log ~ 2 = ~ _{n \to \infty } ^\lim \frac{n}{2}(2^{1/n}-2^{-1/n}),\)
再次,当n = 1,000
x1,000 = 0.693147(236…),
这个误差是\(O(\frac{1} { n ^2})\)。总结本节,我们给出了赛德尔在1871年发布的不寻常的无限乘积公式
\( \displaystyle \frac { log ~ x }{x-1}= \prod _{k=1} ^{k= \infty} \frac {2} {x^\frac{1}{2^k}+1} \)
我们将它应用于x = 2
\( log ~ 2 = \frac{2}{2^{1/2}+1} \frac{2}{2^{1/4}+1} \frac{2}{2^{1/8}+1} \cdots \)
4 泰勒展开
1668年,尼古拉斯·墨卡托(1620-1687)在他的对数函数[6]中发表 了着名的对数函数级数展开式:
定理3 (墨卡托)
\(\displaystyle log (1+x)= x – \frac{x^2}{2} + \frac{x^3}{3} + \cdots= \sum _{k \geq1} \frac{(-1)^{k-1}x^k}{k}. \quad -1<x \leq 1 \)
墨卡托级数与詹姆斯•格雷戈里(James Gregory,1638-1675)研究的另一个级数非常相似:
\( arctan ~ x = x – \frac{x^3}{3} + \frac{x^5}{5} – \cdots \)
第一个使用墨卡托级数的数学家之一是伊莎克·牛顿(Isaac Newton,1643-1727),他在1671年写了着名的“De Methodis Serierum et
Fluxionum”(De Methodis Serierum et Fluxionum),此书包含了各种对数计算,但直到1736年,John Colson才将这本书翻译成英文并发表 。.
他对较小的x值(如± 0.1,1± 0.2)进行了精确的计算,然后使用log 2 = 2log(1.2)- log(0.9)- log(0.8)之类的关系计算大数的对数。.
对x = 1, 应用墨卡托级数会导致着名且慢的收敛
\( log ~ 2 = 1 – \frac{1}{2} + \frac{1}{3} – \frac{1}{4} + \frac{1}{5}- \cdots \)
分别取10,100,1000和10000项得到:
|
x10
|
= | 0.6(456…) |
|
x100
|
= | 0.6(881…) |
|
x1,000
|
= | 0.69(264…) |
|
x10,000
|
= | 0.693(097…). |
一个好得多的想法是应用x = – 1/2 , 这产生了一个经常用于数值计算的公式:
\( \displaystyle log ~2 = \sum _{k \geq1} \frac{1}{k2^k} \qquad (1) \)
这个公式的收敛速度是几何级的(每获得1位数字,需要p次迭代)。
|
x1
|
= | 0.(5) |
|
x10
|
= | 0.693(064…) |
|
x100
|
= | 0.6931471805599453094172321214581(688…) |
应用这个公式,取k = 1000时,log 2的数字超过300位。 获得d位十进制数字所需的迭代次数k由下式给出(在前面的公式中N = 2)
\( \frac{1}{10^d}=\frac{1}{kN^k} \)
这给出了k的上限值
\( k \approx \frac{d}{log10(N)} \)
如果我们使用平凡的分解2 = (4/3) (3/2), 并在等号两端取对数,我们找到一个新的公式
\( \displaystyle log ~ 2= \sum_{k \geq 1} \frac{1}{k} \Big( \frac{1}{3^k}+\frac{1}{4^k}\Big) \)
当K达到1000时,这个级数的部分总和将会超过470位有效数字。
从等式log 2 = – 1 / 2log(1 – 1/4)+ arctanh(1/2)(参见下一段关于arctanh的定义),我们推导出公式
\( \displaystyle log ~2 = \sum _{k \geq 0} \Big ( \frac{1}{8k+8} + \frac{1}{4k+2} \Big ) \frac{1}{4^k}, \)
\( \displaystyle log ~2 = \frac{2}{3} + \sum _{k \geq 1} \Big ( \frac{1}{2k} + \frac{1}{4k+1} + \frac{1}{8k+4} + \frac{1}{16k+12}\Big ) \frac{1}{16^k}. \)这些公式还可以用来直接计算 log 2 的第n个二进制数字,而不用计算以前的数字。
5 Machin类公式
使用墨卡托级数已经大大提高了我们计算log2至很多位数字的能力,但是对于数p来说,可以走的更远。我们记得反双曲正切的定义。我们记
得反双曲正切的定义.
定义4 令| x | < 1:
\( \displaystyle arctanh~x = \frac{1}{2} log \Big(\frac{1+x}{1-x} \Big) = \sum _{k \geq 0} \frac {x^{2k+1}}{2k+1}. \)
对于x = 1/3,这很容易导出与公式 \( \pi = arctan(1) \) 类似的基本公式log 2 = 2 arctanh(1/3)。我们将其重写为:
\( \displaystyle log ~2 = \frac{2}{3} \sum _{ k \geq 0 } \frac{1}{(2k+1)9^k} \)
下面是两个迭代:
|
x1
|
= | 0.6(666…), |
|
x10
|
= | 0.6931471805(498…). |
将公式应用到k = 1000时,log 2的有效数字超过了950位。. 可以做得更好吗?有一个著名的\( \pi \)的 公式,这个公式被称为梅钦的公式,由著名的
关系式子给出:
\( \frac{\pi}{4}= 4~ arctan(\frac{1}{5}) – arctan(\frac{1}{239}).\)
这个想法是寻找计算log2的关系式. 如果我们注意 \( (a_1,a_2,\cdots,a_n)\)这一组有理数和 \( (p_1,p_2,\cdots, p_n)\)这样一组不断增加的整数, 这个关系式是下面这个样子的。
\( \displaystyle log~2 = \sum _{i=1} ^n a_i ~ arctanh(\frac{1}{p_i})\)
我们也希望公式是高效的。一个好的关系式是一个少的项数(n必须小)和大的\(p_i\)的折中。按照莱默的做法,我们通过下面的公式定义效率E.
定义5 (莱默度量)。 令\(p_i > 0\), 是n个元素的数组,则:
\( \displaystyle E = \sum _{i=1} ^n \frac{1}{log10({p_i}^2)} \)
例如log 2 = 2 arctanh(1/3),这里(n=1,p= 3),效率度量是1.05。使用同样的效率定义,Machin公式的效率度量为0.926(n=2, p1=5,p2=239), 所以它比log 2的公式效率更高。
可以推出如下分解定理:
定理6 令p>1 :
\( arctanh ( \frac{1} {p}) = arctanh (\frac{1}{2p-1}) + arctanh(\frac{1}{2p+1}) \)
\( arctanh ( \frac{1} {p}) = 2arctanh (\frac{1}{2p-1}) – arctanh(\frac{1}{2p^2-1}) \)
\( arctanh ( \frac{1} {p}) = 2arctanh (\frac{1}{2p+11}) + arctanh(\frac{1}{2p^2-1}) \)
\( arctanh ( \frac{1} {p}) = 2arctanh (\frac{1}{2p}) + arctanh(\frac{1}{4p^3-3p}) \)
对p = 3 应用这个定理给出了n = 2的关系式
推论7
\( log~2 = 2 arctanh(\frac{1}{5}) + 2 arctanh(\frac{1}{7}) \) Euler 1748 (2)
\( log~2 = 4 arctanh(\frac{1}{5}) – 2 arctanh(\frac{1}{17}) \) (3)
\( log~2 = 4 arctanh(\frac{1}{7}) + 2 arctanh(\frac{1}{17}) \) (4)
\( log~2 = 4 arctanh(\frac{1}{6}) + 2 arctanh(\frac{1}{99}) \) (5)
以上3个公式的效率分别为E = 1.307,E = 1.121,E = 0.998,E = 0.893。 使用其他分解公式和计算机计算,可以找到许多其他的这种性质的关系式(在[8]中给出)。为了说明这一点,我们选择另外几个公式,1个三项的和2个四项的。
定理8 (1997)。常数log 2可以通过以下任何1个快速收敛的级数获得:
\( log~2 = 18 arctanh(\frac{1}{26}) – 2 arctanh(\frac{1}{4801}) + 8 arctanh(\frac{1}{8749}) \) (6)
\( log~2 = 144 arctanh(\frac{1}{251}) + 54 arctanh(\frac{1}{449}) – 38 arctanh(\frac{1}{4801}) + 62 arctanh(\frac{1}{8749}) \) (7)
\( log~2 = 72 arctanh(\frac{1}{127}) + 54 arctanh(\frac{1}{449}) + 34 arctanh(\frac{1}{4801}) -10 arctanh(\frac{1}{8749}) \) (8)
以上3个公式的效率分别是(E = 0.616,E = 0.659,E = 0.689)。最后两个公式用于计算log 2的\(10^8\)位。一个用于计算,另一个用于验证,正如你所看到的,只有5个arctanh的计算是必要的,因为有2项arctanh被重复使用。由于关系(6),几年后的记录增加到了\(5 \times 10^8\)以上。
请注意,还可以分别执行每一项的计算,使这些关系式的计算可以并行化。
例如,我们给出第二个公式的第一次迭代(包含251的那个),每次迭代会增加精度4.8位:
|
x1
|
= | 0.6(456…) |
|
x2
|
= | 0.6931471805(304…) |
|
x3
|
= | 0.69314718055994(497…) |
|
x4
|
= | 0.69314718055994530941(317…) |
5.1有理数的公式
寻找与有理数有关的关系可能是方便的,其形式是同一的:
\( \displaystyle log~2 = \sum _{i=1}^n a_i ~ arctanh( \frac{m_i}{p_i}) \)
\(m_i\)是整数,而上面的公式是1,莱默度量必须考虑这一点。
定理9 (1997)
\( log ~ 2= 6 arctanh(\frac{1}{9}) + 2 arctanh(\frac{3}{253}),\) (9)
\( log ~ 2= 10 arctanh(\frac{1}{17}) + 4 arctanh(\frac{13}{499}),\) (10)
其效率分别为 E = 0.784和 E = 0.722。注意关系式(10)用于几个常数的高精度计算。
6 各种超几何级数
高斯研究了以下级数家族
\( F(a,b,c,z)= 1 + \frac {a \cdot b} {c} \frac{z}{1 ! } + \frac {a(a+1) \cdot b (b+1)}{ c(c+1)} \frac{z^2}{2!} + \cdots \)
其中a,b,c是实数。该级数收敛于 | z | <1.。在圆| z | = 1时,级数在c > a + b时收敛。这些函数被称称之为超几何函数 [1]。通过使用合适的a,b,c的值,许多通常的函数可以表示为超几何函数。
例10
\( ln(1+x)= xF(1,1;2;-x), \)
\( arctanh~x = xF(\frac{1}{2},1;\frac{3}{2};x^2), \)
\( arctan~x = xF(\frac{1}{2},1;\frac{3}{2};-x^2), \)
\( \frac{1}{1-x}= F(1,1;1;x). \)
1797年,高斯的朋友约翰·弗里德里希·普法夫(Johann Friederich Pfaff,1765-1825)给出了有趣的关系式
\( F(a,b,c,z)= (1-z)^{-b} F(c-a,b,c, \frac{z}{z-1} ). \)
如果我们将这个公式应用于arctanh函数
\( arctanh~x = xF(\frac{1}{2},1;\frac{3}{2};x^2), \)
我们发现,
\( arctanh~x =\frac{x}{1-x^2} F(1,1;\frac{3}{2};\frac{x^2}{x^2-1}), \)
对这个函数,我们给出一个新的级数
\( arctanh~x = \frac{x}{1-x^2} \Big ( 1- \frac{2}{3}(\frac{x^2}{1-x^2} ) + \frac{2 \cdot 4 } {3 \cdot 5} (\frac{x^2}{1-x^2})^2 – \frac{2 \cdot 4 \cdot 6}{3 \cdot 5 \cdot 7} ( \frac{x^2}{1-x^2})^3 + \cdots \Big ) \)
使用 log2 = 2 arctanh(1/3); 经过一些简单的操作,该级数
推论11
\( log 2 = \frac{3}{4} \Big ( 1- \frac{1}{12} + \frac{1 \cdot 2}{12 \cdot 20}- \frac{1 \cdot 2 \cdot 3}{12 \cdot 20 \cdot 28} + \cdots \Big ). \)
这个级数的每个新项都乘以- k /(8 k +4),其中k = 1,2,…欧拉给出了同样类型的公式来计算\( \pi \)。这个推论的一个很好的应用就是编写一个很小的代码来计算log 2,就计算\( \pi \)一样。
7. log2和AGM
所有先前的级数的收敛率是对数或几何的。根据AGM(算术几何平均值)(参见[2]),可以找出一个计算log 2的公式,这个公式就像\( \pi \)一样,是二次收敛的。
基于AGM的二次收敛算法中最经典的log 2如下所示。从开始一个\(a_0\)和 \(b_0>0 \),我们考虑AGM迭代
我们使用符号
\( a_{n+1}=\frac{a_n+b_n}{2}, \qquad b_{n+1}= \sqrt {a_n b_n }, \)
我们使用迭代
\( \displaystyle R(a_0,b_0)= \frac{1} {(1- \sum _{n \geq 0} 2^{n-1}( {a_n}^2-{b_n}^2) )} \)
定理12 令 \( N \geq 3\) 和 \( x \leq 1\)
\( \vert log ~ x – R(1,10^{-N}) + R(1,10^{-N}) x \vert \leq \frac{N}{10 ^{2(N-2)}}\)
通过选择x = 1/2,该算法给出log 2的约2N位十进制数。这个是二次收敛的,并且当 \(2^{n-1} ( {a_n}^2 – {b_n}^2 \)小于 \(10^{-2N} \) 就该停止,为 \( n \approx log_2(N) \)
请注意,这个算法不是专门用来计算log2的,对于任何实数X,都可以用来计算logX的值。. 使用FFT乘法,以获得 n位有效数字的x,它的复杂性是O(n log^2n)。
8 计算log p
从log 2的一个很好的近似开始,由于这个关系式的缘故,很容易找到所有整数的对数的表达式
\( \displaystyle 2 ~ arctanh( \frac{1}{2p+1}) = log \Big ( \frac{1+\frac{1}{2p+1}}{1-\frac{1}{2p+1} } \Big )= log( \frac{p+1}{p}), \)
因此我们推断:
定理13 令p> 0
\( log(p+1)= log ~ p + 2 \Big ( \frac{1}{2p+1} + \frac{1}{3} \frac{1}{ {(2p+1)}^3} + \frac{1}{5} \frac{1}{ {(2p+1)}^5} + \cdots \Big ) . \)
当你需要计算多个连续的整数的对数时,这可能是有用的。
实例14 用p=2,p=4 和p=7
\( log ~ 3 = log ~ 2 + \frac{2}{5} \Big ( 1+ \frac{1}{3} \frac{1}{25} + \frac{1}{5}\frac{1}{25^2} + \cdots \Big ),\)
\( log ~ 5 = 2log2 + \frac{2}{9} \Big ( 1+ \frac{1}{3} \frac{1}{81} + \frac{1}{5}\frac{1}{81^2} + \cdots \Big ), \)
\( log ~ 7 = 3log2 + \frac{2}{15} \Big ( 1+ \frac{1}{3} \frac{1}{225} + \frac{1}{5}\frac{1}{225^2} + \cdots \Big ). \)
9 log2公式的集合
log2的积分和级数公式可以在log2的公式集合中找到。
10 log 2的计算记录
| 位数 | 什么时候 | 谁 | 备注 |
| 16 | 约1671 | 牛顿 | 他用log2 = 2log(1.2)-log(0.9)-log(0.8)和墨卡托级数对数。 |
| 25 | 1748 | 欧拉 | 关系式(2)被使用。欧拉还计算了整数3 到10的的自然对数,并精确到25位有效数字[5]。 |
| 137 | 1853 | Shanks | 还计算了log3,log5和log10的值,并精确到137位数字。他的工作发表了一个p计算[9]。 |
| 273 | 1878 | 亚当斯 | 亚当斯还以相同的精度计算了log3,log5和log7。 |
| 330 | 1940 | H. S. Uhler | 罗康瑞还使用相同的精度,计算出了log3,log5,log7和log17的值[11]。 |
| 3 683 | 1962 | D.W. Sweeney | 在同一篇文章指出,计算log2是计算欧拉常数最多达3566位的必要条件)。 用于log2的公式是扩展(1)(见[10]) |
| 2 015 926 | 1997 | P. Demiche | 他的计算使用公式(2)这个经典方法。HP9000 / 871在160MHz下花了16个小时。 |
| 5 039 926 | 1997 | P. Demiche | 同样的技术被使用,在同一台计算机上做计算,花了130个小时 |
| 10 079 926 | 1997年12月 | P. Demiche | 相同的技术,在同一台计算机上做计算,400小时。 |
| 29 243 200 | 1997年12月 | X. Gourdon | 使用AGM公式(11),用到FFT技术。计算是在SGI R10000工作站上完成的,耗时20小时58分钟。 |
| 58 484 499 | 1997年12月 | X. Gourdon | 相同的AGM技术,在同一台计算机上83小时。 |
| 108 000 000 | 1998年9月 | X. Gourdon | 四项公式(7)与二分法一起使用。公式(8)被用于验证。在一台具有256M内存PII 450,这个算过程化 了47个小时的。 |
| 200 001 000 | 2001年9月 | X. Gourdon 和 S. Kondo | 使用公式(6)和(5)。 在一台具有256M内存的Athlon 1300,花了8个小 时。 |
| 240 000 000 | 2001年9月 | X. Gourdon 和 S. Kondo | 使用公式(6)和(10)。在一台具有1024M内存的PIV 1400上,花了14个小 时. |
| 500 000 999 | 2001年9月 | X. Gourdon 和 S. Kondo | 使用公式(6)和(10)。在一台具有1024M内存的PIV 1400上,花了28个小 时. |
参考文献
[1] M. Abramowitz and I. Stegun, Handbook of Mathematical Functions, Dover, New York, (1964)
[2] J.M. Borwein and P.B.Borwein, “Pi and the AGM – A study in Analytic Number Theory and Computational Complexity”, A
Wiley-Interscience Publication, New York, (1987)
[3] R.P. Brent, Fast multiple-Precision evaluation of elementary functions, J. Assoc. Comput. Mach., (1976), vol. 23,
p.242-251
[4] H.Briggs, Arithmetica logarithmica sive logarithmorum Chiliades Triginta, London, (1624)
[5] L. Euler, Introduction à l analyse infinitésimale (french traduction by Labey), Barrois, aîné, Librairie, (original
1748, traduction 1796), vol. 1, p. 89-90
[6] N. Mercator, Logarithmotechnia, London, (1668)
[7] J. Napier, Mirifici logarithmorum canonis descriptio, Edimboug, (1614)
[8] P. Sebah, Machin like formulae for logarithm, Unpublished, (1997).
[9] W. Shanks, Contributions to Mathematics Comprising Chiefly the Rectification of the Circle to 607 Places of Decimals,
G. Bell, London, (1853)
[10] D.W. Sweeney, On the Computation of Euler’s Constant, Mathematics of Computation, (1963), p. 170-178
[11] H.S. Uhler, Recalculation and extension of the modulus and of the logarithms of 2, 3, 5, 7 and 17, Proc. Nat. Acad.
Sci., (1940), vol. 26, p. 205-212
[12] A. Vlacq, Arithmetica logarithmica, Gouda, (1628)
