发布于

重磅消息–一种新的任意精度对数算法研究成功

经过许多个月的艰辛努力，我自己独立开发的高精度算术库（BCMP）终于可以告一段落了。另外，由我自己独创的对数log(x)算法也已经完成。测试报告显示，这个算法的性能是非常令人振奋的，在100-10000位精度下，可比现在最快软件Mathematica[注9]快2.8到8倍。

BCMP和GMP[注1]类似，利用BCMP可以计算任意精度整数和浮点数的算术运算，包括加，减，乘，除，开平方等。和GMP类似，我开发这套大数库的主要目标为追求极致的性能。现在，这一目标已基本达到。在中等精度（1万位十进制）以下，BCMP在大多数情况下，显著领先于GMP。当精度更高时，bcmp则慢于GMP，这是因为，大数运算库的关键是乘法，而不同大小的操作数需要使用不同的算法，没有一种算法可以适应于任意情况。BCMP中实现了basecase乘法[注2]，karatsuba乘法[注3]，Toom-Cook[注4]系列乘法，而尚未实现适应于操作数很大的SSA[注5]算法，或者FFT[注6]算法和NTT[注7]算法。和GMP不同，BCMP提供了2套接口，第一套接口支持2进制运算，内部表示采用\(2^{30}\)进制，另一套接口支持10进制运算，内部表示采用\(10^9\)进制。BCMP计划同时支持32位和64位方式编译，也计划同时支持在windows下编译和Linux下编译。现在已实现32位模式下的用Visual Studio编译，今后将逐步完善其他功能。

BCMP主要使用C语言和汇编语言开发，为了实现极高的性能，使用了大量的汇编代码，对关键部分做了精心的优化，除了普通的汇编指令外，还大量使用SSE2，SSE4和少数AVX2指令。

新的任意精度对数函数算法是我独创的，不同于任何一个公开发表的算法。新算法基于质数分解和比特突发算法，大大加速了计算速度，从算法复杂度来说，它和目前最快的算法AGM算法[注8]有相同的复杂度，都是O(log(P)M(P)),p为精度，其中M(P)代表两个P位整数相乘所需要的基本运算的次数。但是我的算法有更小的常数因子，速度更快。下表列出了几个最著名数学软件和大数库与BCMP在计算log(x)的性能对比结果。从这个表中可以看出，当精度为100到10000位时，我的新算法是MPFR[注11]的3.7到8.6倍

测试平台：
处理器: Intel(R) Core(TM) i7-2600K CPU @3.40GH
操作系统: Windows7 32-bit
Maple[注10] 版本：17.0
Mathematica版本： 10.3.0 32-bit
Pari[注12]版本： 2.9.3
mpfr版本：3.1.6

 

位数 时间，单位为毫秒
Maple Mathematica Pari MPFR BCMP_log1 BCMP_log2
20 0.029941 0.00247424 0.003114 0.004833 0.008654 0.000762
30 0.040354 0.00305579 0.003744 0.005667 0.008218 0.000975
40 0.043768 0.003999 0.004687 0.006456 0.010237 0.001043
50 0.045405 0.00464357 0.005267 0.006782 0.010515 0.001217
60 0.061336 0.00551004 0.007068 0.008939 0.012052 0.002432
70 0.063722 0.00660306 0.008129 0.009373 0.012467 0.002622
80 0.06523 0.00748533 0.008918 0.010451 0.014011 0.002847
90 0.067488 0.00873332 0.009401 0.010859 0.013989 0.002967
100 0.069835 0.00976343 0.011404 0.012145 0.017113 0.003194
125 0.072167 0.0121835 0.013434 0.014376 0.020085 0.003843
158 0.079578 0.0186991 0.020295 0.018568 0.026015 0.004825
199 0.084953 0.0257783 0.027464 0.023096 0.032686 0.005604
251 0.101058 0.0337484 0.039437 0.030076 0.041313 0.006338
316 0.111391 0.0496319 0.057234 0.03874 0.057398 0.008075
398 0.125592 0.0655544 0.090215 0.054713 0.076384 0.009971
501 0.140205 0.0873334 0.126219 0.076801 0.100851 0.012947
630 0.169863 0.143491 0.173471 0.1227 0.126775 0.025564
794 0.201257 0.213486 0.262401 0.192741 0.175562 0.022624
1000 0.26965 0.331134 0.378275 0.29729 0.260477 0.041692
1258 0.344599 0.4512 0.545905 0.425357 0.321757 0.056777
1584 0.437988 0.615793 0.836217 0.671066 0.504561 0.077545
1995 0.570668 0.871282 1.219222 1.042976 0.671209 0.133183
2511 0.807129 1.20226 1.723848 1.448282 0.983084 0.190615
3162 1.07266 1.68033 2.561828 2.257336 1.489376 0.273305
3981 1.47754 2.42274 3.66907 2.959093 2.155975 0.510987
5011 2.15234 3.27768 5.208427 3.788049 3.193957 0.727249
6309 2.96615 4.7273 7.723928 5.709551 4.507839 1.019573
7943 4.0625 6.69787 11.071721 7.894751 6.753858 1.748821
10000 6.33854 9.14068 15.950279 10.198301 9.649934 2.538205
17782 15.1146 21.4501 38.916218 23.862088 23.569465 6.929607
31622 42.25 56.5504 94.352581 68.980759 62.309453 18.861327
56234 681 117.001 207.879794 131.337302 146.628323 45.943156
100000 2012.67 260.002 587.256462 296.982964 364.771994 117.998387

性能对比折线图，以mpfr为基准，令mpfr的运行时间为1，值越小越好。

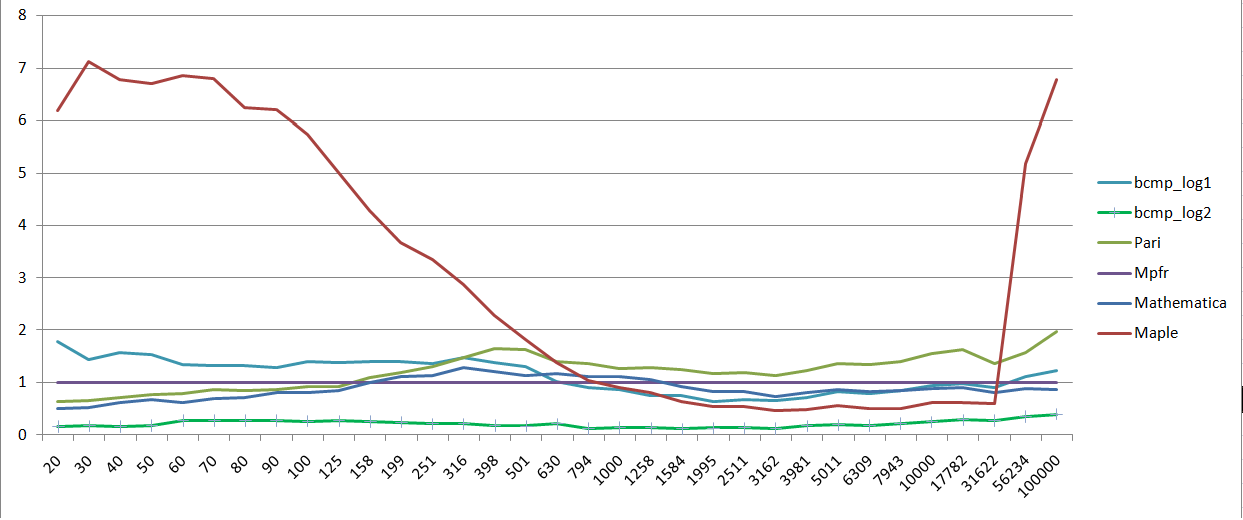
性能对比折线图2，去掉Maple的测试结果，仍以mpfr为基准，值越小越好。

说明：BCMP用两种方法实现了两个版本的log函数，第一个使用AGM算法，在上表中标记为BCMP_log1, 第二个使用新算法，标记为BCMP_log2

测试代码下载：
mathematica,maple,pari,mpfr,bcmp,time

测试结果下载：
test_result
更多的任意精度浮点软件性能比较，请参阅Comparison of multiple-precision floating-point software

1.GMP是一个用于任意精度算术的免费库，用于对有符号整数，有理数和浮点数进行操作。GMP的主要目标应用是密码应用和研究，互联网安全应用和计算机代数系统。GMP是一个非常优秀的大数库，已有26年的历史。GMP的作者曾宣称，GMP是地球上最快的大数库,原文“the fastest bignum library on the planet!”。因为GMP非常快，所以很多应用软件使用GMP，如计算机代数系统Mathematica和Maple中的整数运算就是调用GMP来实现的。
关于GMP更多的信息，请参阅https://gmplib.org 和 https://en.wikipedia.org/wiki/GNU_Multiple_Precision_Arithmetic_Library

2.basecase乘法，也叫长乘法(Long multiplication),请参阅 https://en.wikipedia.org/wiki/Multiplication_algorithm

3.Karatsuba乘法，也称Karatsuba算法，这个算法由Anatoly Karatsuba在1960年发现的， 是一种比长乘法更快的算法，请参阅https://en.wikipedia.org/wiki/Karatsuba_algorithm。

4.Toom–Cook乘法，狭义的Toom-Cook算法指Toom-3算法，可以看做是Karatsuba乘法的推广。广义的Toom-Cook乘法包括Toom4，Toom5等一大类算法。这个算法最早由俄罗斯数学家Andrei Toom提出，而Stephen Cook(是美国和加拿大计算机科学和数学家，图灵奖的获得者）给出更清晰的描述，请参阅维基百科https://en.wikipedia.org/wiki/Toom%E2%80%93Cook_multiplication

5.SSA算法指Schönhage–Strassen algorithm ，他是德国数学家和计算机科学家Arnold Schönhage和德国数学家Volker Strassen在1971开发出来的一个算法。关于这个算法的更多信息，请参阅维基百科https://en.wikipedia.org/wiki/Sch%C3%B6nhage%E2%80%93Strassen_algorithm 和百度百科https://baike.baidu.com/item/SSA/18691142，原始论文请参阅《A GMP-based Implementation of Schönhage-Strassen’s Large Integer Multiplication Algorithm》

6.FFT指快速傅里叶变换（fast Fourier transform），是基于复数的一种线性变换，这个算法在电子技术领域得到极其广泛的应用，是20世纪10大算法之一。另外，这个算法可用来计算大数乘法。关于FFT的更多信息，请参阅 https://en.wikipedia.org/wiki/Fast_Fourier_transform。关于20世纪10大算法，请参阅http://science.dataguru.cn/article-9643-1.html

7.NTT指数论变换(Number-theoretic transform)，它是FFT推广到有限域上的一种变换算法，和FFT不同，他不使用复数域上的加，减和乘法，而是使用模算术。apfloat中的大数乘法用的就是NTT算法。感兴趣的读者可以参阅蒋增荣的《数论变换》或者孙琦的《快速数论变换》等书。

8.AGM指算法几何平均数，关于这个算法的描述请参阅澳大利亚数学家和计算机科学家Richard P. Brent《Fast Algorithms for High-Precision Computation of Elementary Functions》和的Borwein兄弟的《The arithmetic-geometricmean and fast computation of elementary functions》和。Borwein兄弟都是数学家，他们出生在苏格兰。

9.Mathematica 是一款功能强大的科学计算软件，和MATLAB、Maple 并称为三大数学软件。请参阅百度百科
https://baike.baidu.com/item/Mathematica

10.Maple和Mathematica类似，也是一款功能强大的科学计算软件。请参阅百度百科https://baike.baidu.com/item/maple/2306572

11.MPFR是基于GMP的一套2进制浮点库，请参阅维基百科https://en.wikipedia.org/wiki/GNU_MPFR

12.PARI/GP是一个计算机代数系统，请参阅维基百科https://en.wikipedia.org/wiki/PARI/GP

发布于

最短的计算大数乘法的c程序

说明：
1.这个程序接收2个从键盘输入的整数，计算他们的乘积，并输出结果。输入的两个整数的总长度不能大于99.
2.这个程序没什么大用，只是用来玩玩儿而已。
3.这个程序的主要目标是,使用尽可能短的代码来实现大数乘法。上面的代码
可在VC下编译并运行. 在GCC下编译，可省略#include语句和void关键字，
去除回车和不必要的空格，总长度仅仅194个字节。
另外，程序刻意避免使用数组来存贮中间结果和最终结果。
为此，使用了递归函数，同时，递归的使用也简化了代码。
4.在实际工作中，千万不要写这样的程序，否则会被骂死。
5.不要用这个程序考你的学生和面试者，即使他宣称精通C语言。

此类最短程序的特点
1.经常使用全局变量，全局变量的优点是
1).自动初始化数组和单变量为0，可省去某些变量初始化语句。
2).数组初始化为0也使得逻辑更简单，可省去某些边界值的判断。
3).在子程序，直接使用全局变量可省去某些参数定义和参数传递语句。

2.在表达式，大量使用“++”或者“–”之类运算符，此类语句往往起到
一箭双雕的效果，可有效的缩短代码长度.但在工作中，我强烈反对使用
这类运算符。

3.在比较语句中，很少使用if(i>0)这类语句，而是使用“if(i)”这样的
写法，这种写法比”>0″少了2个字母。

发布于

AGM函数近似值的估计

AGM是 Arithmetic-Geometric Mean的缩写，意为算术几何平均数。其定义为,给定两个正实数a0和b0，我们定义一个迭代过程

\( a_{i+1}= \frac {a_i+b_i} {2}, \qquad b_{i+1}= \sqrt {a_i \cdot b_i } \)

前者求两个数的算术平均数，后者求2个数的几何平均数。这两个序列有同样的极限，其值表示为A(a0,b0)，在AGM迭代过程中，序列收敛地非常快，一旦\(a_i\) 和\(b_i\)大小相近时，每迭代一次，有效数字加倍。下表显示了这两个序列的收敛速度[1]

n \(a_n\) \(b_n\)
0 24 6
1 15 12
2 13.5 13.41640786499873817845
3 13.45820393249936908922 13.45813903099098487720
4 13.45817148174517698321 13.45817148170605385831
5 13.45817148172561542076 13.458171481725615420761

高斯发现，AGM函数可以用来求椭圆积分的值

\( A(1,x)= \frac{\pi} {2F(x)} \)

F(x)为椭圆积分函数

\( \displaystyle \int_0^{\pi \over 2} \frac{d\theta} { \sqrt {1-(1-x^2 ) \sin^2 \theta)}} ) \)

AGM函数不但可以快速的计算椭圆积分，也可用来计算对数函数ln(x).
[2]给出一个椭圆积分F(x)和对数函数ln(s)的关系式

\(
F(\frac{4}{s})=\ln(s)+ \frac{4\ln(s)-4}{s^2}+\frac{36\ln(s)-42}{s^4} + \frac{1200 \ln(s)-1480}{3s^6} + O(\frac{1}{s^8}) \)

如果s是足够的大，F(4/s)是非常好的ln(s)的近似值。为了计算ln(s)到p位2进制数。s必须大于\(2^{p \over 2 } \)。故为了计算ln(x),我们首先需要找到一个实数s和整数m，使得

\( s=x \cdot2^m \gt 2^{p \over 2} \)

[2]给出如下求ln(x)的公式

\( \displaystyle ln(x)=\frac{\pi}{2A({4 \over s},1)} -m \ln (2) \qquad (1)\)

我们将这个公式稍作一下变形

\( \displaystyle \ln(x)=\frac{{1 \over 8}\pi s}{A({s \over 4},1)} -m \ln (2)= \frac{{1 \over 2}\pi \cdot x \cdot 2^{m-2}}{A(x \cdot 2^{m-2},1)} – m \ln(2)
\qquad  (2) \)

反过来，利用这个公式，我们可以求AGM(1,y)的近似值，这里要求y>>1。在公式(2)中，我们取x为1，这样不但可以消去方程中的x，也可以消去ln(x)，这样公式(2)变为

\(  \displaystyle \frac {{1 \over 2} \pi \cdot 2^{m-2}}{A(2^{m-2},1)}=m \ln(2) \quad (3)\)

令 \(y=2^{m-2}\), 则

\( \displaystyle A(y,1)= \frac { {1 \over 2} \pi \cdot y} {(log2(y)+2) \ln 2} = y \frac{{1 \over 2} \pi / \ln(2)}{log2(y)+2} \approx y \frac{2.26618007091}{log2(y)+2} \quad    (4) \)

下表是y取某些值时，使用公式(4)得到的近似值和真实值的对比。我们可以发现，当y>10,这个近似公式可以精确到3位以上有效数字。

y A(y,1) 公式(4)
10 4.25040709493 4.25819370444
\(2^4\) 6.03865834042 6.04314685577
\(2^6\) 18.1285335082 18.1294405673
\(2^8\) 58.0140204356 58.0142098154
\(2^{16}\) 8250.90983997 8250.90984041
\(2^{24}\) 1462315.09787 1462315.09787
\(2^{32}\) 286269685.042 286269685.042

参考文献
[1] agm(24, 6) at WolframAlpha. http://www.wolframalpha.com/input/?i=agm%2824%2C+6%29
[2] Muller J M. Elementary Functions: Algorithms and Implementation[M]. Springer Science+Business Media New York, 2016,130-131